About Trisicell
Trisicell is a computational toolkit for scalable intratumor heterogeneity inference and validation from full-length transcriptome profiling of single-cell data (e.g. Smart-seq2) as well as single cell genome or exome sequencing data. Trisicell allows identifying and validating robust portions of a tumor progression tree, offering the ability to focus on the most important (sub)clones and the genomic alterations that seed the associated clonal expansion.
Tumor Progression Tree Reconstruction Models
Cancer is an evolutionary process. Looking back in time there were somatic mutational events that resulted in an emergence of the first cancerous cell. By the means of cell division, the number of cancerous cells grew, and newly born cells acquired additional mutations over time, which results in distinct populations of cells, each with its own complement of somatic mutations. Consequently, tumors are typically heterogeneous and are made of these different populations of cells. The heterogeneity provides the fuel for resistance either to the therapy or to the immune system. Single-cell sequencing (SCS) provides high resolution data that enables studying tumor progression tree and heterogeneity at unprecedented detail.
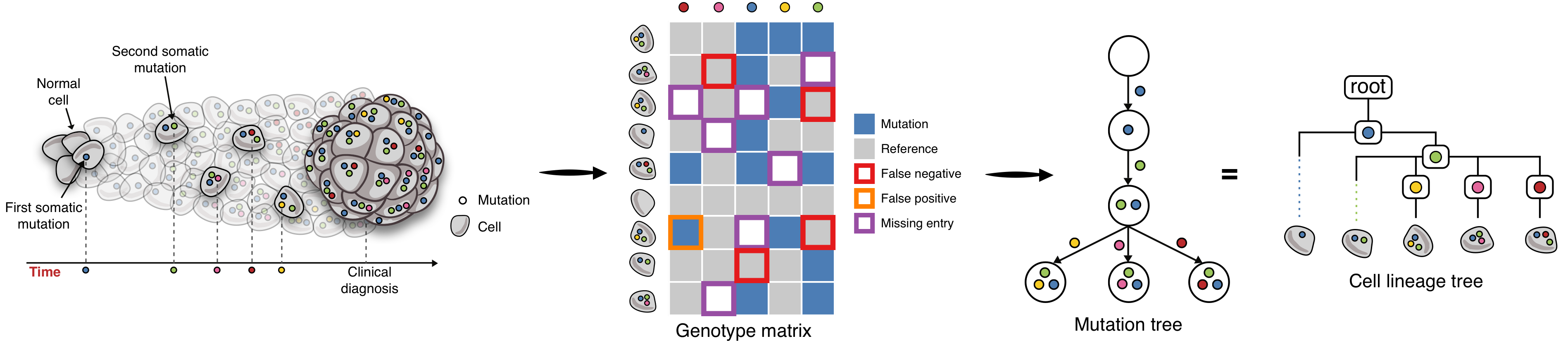
After mutation calling in every cell obtained by SCS, we have a matrix where rows represent individual cells and columns represent somatic mutations. The entries of the matrix show the presence/absence of mutations in cells. This matrix is better known as the genotype matrix. There are several types of noise present in the observed single-cell genotype matrix and they include:
- False-negative errors
where a mutation is actually present in the cell but due to allele dropout (either biological or technical) or variance in sequencing coverage, in the genotype matrix it is reported as absent in the cell
- False-positive errors
where a mutation is absent in the cell but in the genotype matrix it is reported to be present
- Missing entries
where some entries contain no information about mutation presence or absence. Their presence in the matrix is usually due to insufficient coverage or lack of expression at the mutated loci in the cell
Due to the presence of false positive and false negative mutation calls, in most cases, the observed matrix contains a triplet of cells and a pair of columns such that in one of the three cells both mutations are reported to be present, in one of them it is reported that only the first mutation is present and in the remaining cell it is reported that only the second mutation is present. We say that such a triplet of cells and a pair of mutations form a conflict. These conflicts prevents us from reconstructing the tree of tumor progression directly from the observed matrix and requires the development of automated computational methods for finding the trees that best match the observed data.
There are several techniques and methods to remove the noise/conflicts from the input genotype matrix. They are mostly based on Integer Linear Programming (ILP), Constraint Satisfaction Programming (CSP), Markov chain Monte Carlo (MCMC) sampling and Neighbor Joining (NJ). For more details, we highly recommend to read our Trisicell and review papers about building tumor progression tree by exploring the space of binary matrices.
Trisicell Components
Trisicell is comprised of three computational methods of independent but complementary aims and applications:
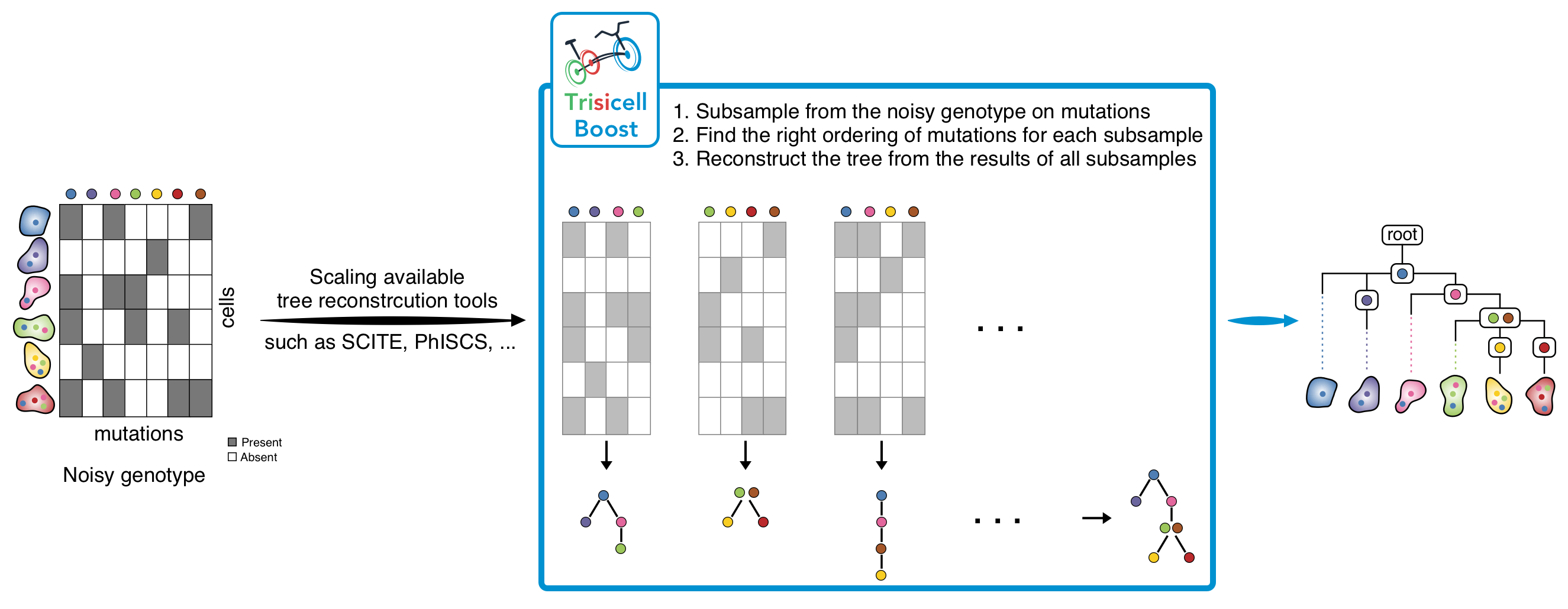
1) Trisicell-Boost:
Trisicell-Boost is a booster for phylogeny inference methods allowing them to scale up and handle large and noisy scRNAseq datasets.
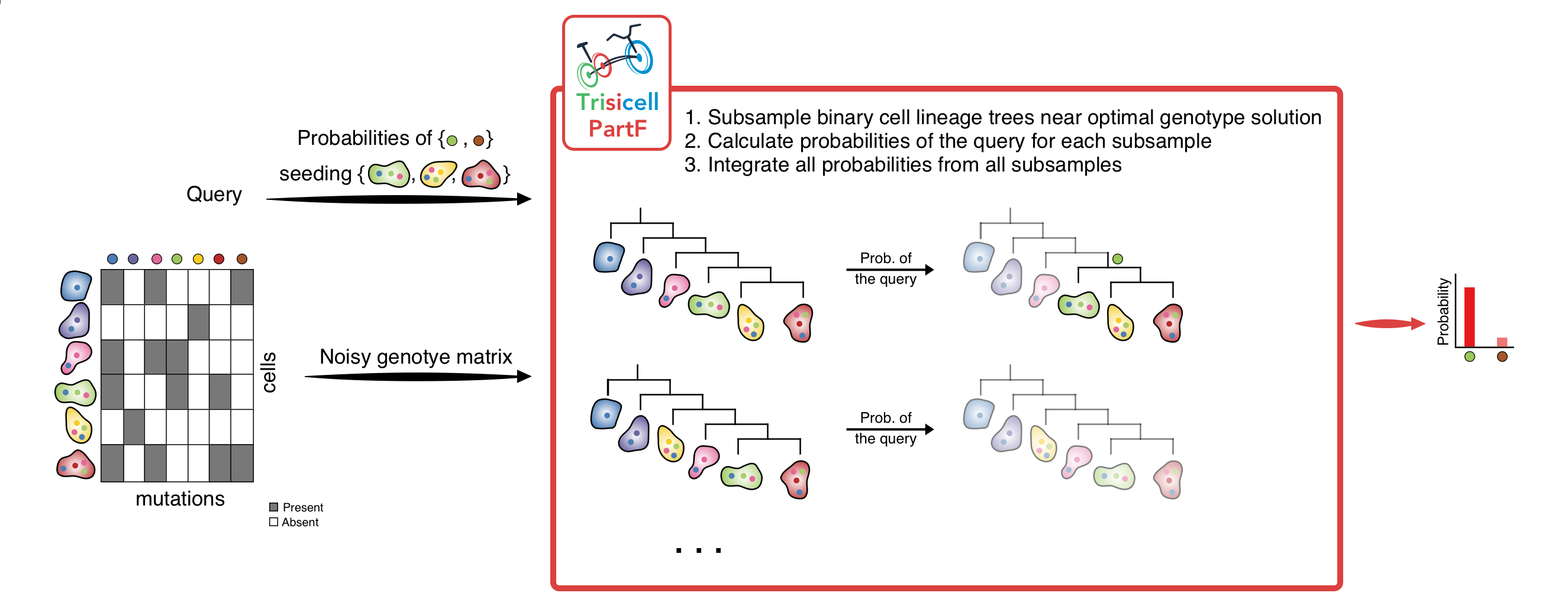
2) Trisicell-PartF:
Trisicell-PartF employs a localized sampling strategy to compute the probability of any user-specified set of cells forming a subclone seeded by one or more (again user- specified) mutations.
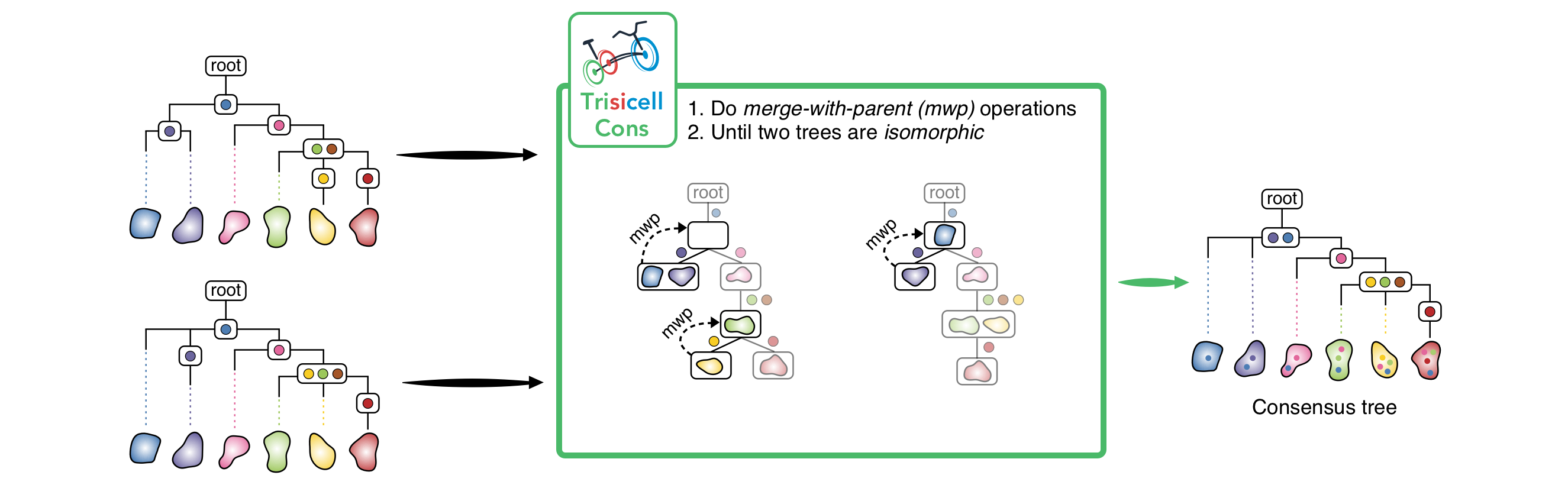
3) Trisicell-Cons:
Trisicell-Cons is devised to compare two or more phylogenies (more specifically cell-lineage trees) derived from the same single-cell data, and build their consensus tree by “collapsing” the minimum number of their edges so that the resulting trees are isomorphic